Při čtení této kapitoly hledejte odpovědi na následující otázky:
- Jak změny v produkci ovlivňují životní úroveň?
- V jakém vztahu jsou produktivita a produkce?
- Jak je možné zlepšit produktivitu a kvalitu?
- Proč se výrobní náklady mění se změnou výstupu?
Ekonomové říkají, že primárním cílem každé firmy je vytvořit největší možný zisk, nebo jinak řečeno, maximalizovat zisky. Pokud by si firma počínala jinak, byla by brzy z podnikání vyřazena. Kdyby se firma snažila maximalizovat své ztráty, nebyla by schopna platit účty. Podobně, kdyby se snažila maximalizovat výrobu, bylo by vyrobeno víc, než by mohlo být prodáno, a firma by opět zhatila peníze.
Jednou z prvních věcí, které firma musí rozhodnout při hledání zisku, je úroveň její produkce. Jak se však zisk měří? Celkový zisk firmy je rozdíl mezi výnosy z prodeje produktu a náklady na výrobu produktu.
Celkový příjem - celkové náklady = celkový zisk
Firma si vybrala úroveň produkce v bodě, v němž dosahuje největšího zisku. Ten nemusí být nezbytně stejný jako nejvyšší možná úroveň produkce.
Po analýze trhu odhalila pekárna koblih Karla Bednáře toto:
| Denní produkce | Zisk |
| 50 krabic | 900 Kč |
| 75 krabic | 1 200 Kč |
| 100 krabic | 1 050 Kč |
Kdybyste byli manažerem pekárny, kolik krabic koblih byste denně produkovali: 50, 75 nebo 100? V tomto případě má smysl produkovat 75, protože to vynese největší zisk.
Jak firma nalezne úroveň výstupu, která maximalizuje zisk? Jeden způsob by spočíval v metodě pokusu a omylu. To znamená, že pekaři mohou usmažit první den jednu krabici koblih, druhý den dvě a tak dále, dokud nedosáhnou svého maximálního denního výstupu. Pokus a omyl je nákladný postup, který zbytečně zabírá čas. Snadnější metoda je založena na tom, co ekonomové nazývají marginální analýzou.
Marginální analýza používá pero a papír, aby zjistila, co se stane, když se firma rozhodne produkovat o jednu jednotku výstupu navíc. Pokouší se provést to, o co se snažila metoda pokusu a omylu, avšak bez zdržování pekárny. Dělá se to takto: pokud výroba dodatečné koblihy přispěje k zisku pekárny, vyplatí se tuto koblihu usmažit. Pro ekonoma je důchod z výroby dodatečné jednotky mezním příjmem. Mezní zisk je vypočítán jako rozdíl mezi mezním příjmem a mezními náklady:
Mezní příjem - mezní náklady = mezní zisk
Mezní příjem je dodatečný příjem, který firma vytvoří, když vyrobí o jednotku výstupu navíc. Obecně mezní příjem klesá, jak se výroba zvyšuje, protože firmy musí nakonec snížit ceny, aby více prodaly.
Mezní náklady jsou náklady firmy na výrobu dodatečné jednotky výstupu. Jak se produkce zvyšuje, mezní náklady nejprve klesají, ale pak se zvyšují. To proto, že bod největší efektivnosti firmy leží někde mezi úrovní minimálního a maximálního výstupu. Jak se výstup zvyšuje směrem k tomuto bodu, výrobní náklady na každou dodatečnou jednotku (její mezní náklady) klesají. Jakmile je dosaženo bodu maximální efektivnosti, dostaví se klesající výnosy a mezní náklady se zvýší.
Mezní zisk je rozdíl mezi mezním příjmem a mezními náklady. Tak jako mezní náklady a mezní příjem, i mezní zisk bude kladný do určité úrovně výstupu a pak se stane záporným. („Záporný zisk“ je jiný název pro ztrátu.)
Jak firma vypočítá úroveň produkce maximalizující zisk?Pokud výroba dodatečné krabice koblih přispěje více k celkovému příjmu než k nákladům, měla by ji firma vyrobit. Pokud výroba dodatečné krabice koblih přispěje méně k příjmu než k nákladům (mezní zisk je záporný neboli menší než nula), neměla by ji firma snažící se o maximální zisk vyrábět.
Protože se mezní zisk obecně mění z kladného na záporný, jakmile výroba překročí bod, kde práce a stroje jsou nejefektivnější, výstup maximalizující zisk odpovídá přesně té úrovni, kde je mezní zisk nulový.
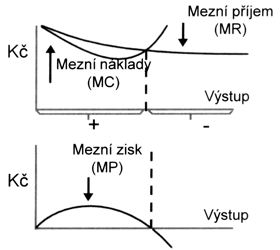
Tím má firma jednoduché pravidlo, podle kterého může provádět svá výrobní rozhodnutí. Měla by zvyšovat výstup až k bodu, v němž mezní příjem = mezní náklady.
Graf ukazuje, jak mezní náklady rostou, a mezní příjem klesá, jakmile naše pekárna zvyšuje svůj výstup koblih. Mezní zisk, jak nyní víme, je rozdíl mezi oběma křivkami. Proto graf ukazuje, že mezní zisk klesá výstupem a nakonec se stává záporným, když mezní náklady jsou větší než mezní příjem. Nyní je jasné, proč firma chce produkovat až k bodu, kde se mezní příjem rovná mezním nákladům. Až do tohoto bodu firma stále zvyšuje zisk, přispívá k jeho růstu. Za tímto bodem se zisk stává menším, neboť mezní zisk přechází do záporných hodnot.
Náklady a výnosy - proč se výrobní náklady mění se změnou výstupuJak firma roste a zvyšuje svůj výstup, dosahuje bodu, v němž produkovat jeden každý výrobek stojí méně, než když firma byla menší. Ale proč? Proč by se měly náklady na výrobu každé jednotky měnit se změnou výstupu? Pro odpověď analyzujme dva různé druhy nákladů, které vstupují do výroby.
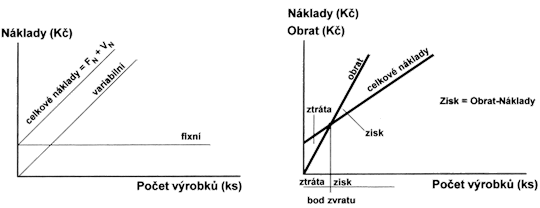
Celkové náklady jsou tvořeny fixními náklady a variabilními náklady.
Firma VAN se zabývá výrobou vozíků. Společnost vlastní malý výrobní závod s kapacitou 10 000 vozíků ročně. Kapacita firmy udává maximální počet jednotek, které může vyrobit. Kdyby firma VAN chtěla vyrábět více než 10 000 vozíků, mohla by to udělat tak, že by rozšířila své prostory, nakoupila nové stroje, vybudovala nový závod nebo udělala nějaká jiná zlepšení ve svém provozu.
Fixní náklady jsou takové, které zůstávají stejné bez ohledu na množství firmou vyráběných jednotek (pro určitý rozsah výrobní kapacity – poté se změní skokem). Příkladem fixních nákladů je nájemné, daně z nemovitostí, plat ředitele a úrok z půjčky.
Účetní firmy VAN vypočítal, že fixní náklady společnosti jsou 1 200 000 Kč za rok.
Variabilní náklady se zvyšují nebo snižují spolu s objemem výroby. Výkonové mzdy, energie a suroviny jsou příklady variabilních nákladů.
Kromě fixních nákladů bude firma VAN také muset krýt variabilní náklady. Když jdou obchody špatně, může VAN propustit dělníky, zastavit provoz některých svých strojů a nakupovat méně surovin. Když se obchody zvýší, vzrostou i tyto položky výdajů.
Jednoho dne se Pavel Vaněk, majitel firmy, zeptal svého účetního, jaké budou pravděpodobné průměrné náklady pro tento rok. „To závisí na tom, kolik vozíků vyrobíte,“ odpověděl účetní. „Co s tím má co dělat vyráběné množství? Já chci jenom znát své průměrné náklady. Náklady na každý jednotlivý vozík, chápete?“
„Já tomu rozumím, pane Vaňku,“ odpověděl účetní. „Dovolte mi, abych vám ukázal výsledky analýzy nákladů, kterou jsme právě dokončili. Uvidíte, co mám na mysli.“ S těmito slovy účetní vytáhl tabulku.
„Hm,“ zamumlal pan Vaněk, když si prohlédl čísla. „Myslím, že byste mi měl radši vysvětlit, co to všechno znamená.“
Účetní vysvětlil panu Vaňkovi, že celkové výrobní náklady jsou součtem fixních nákladů a variabilních nákladů.
| (1) Vyrobené vozíky | (2) Celkové fixní náklady | (3) Průměrné fixní náklady | (4) Celkové variabilní náklady | (5) Průměrné variabilní náklady | (6) Průměrné celkové náklady |
|---|---|---|---|---|---|
| 0 | 1.200.000 | 0 | |||
| 1.000 | 1.200.000 | 1.200 | 700.000 | 700 | 1.900 |
| 3.000 | 1.200.000 | 400 | 1.200.000 | 400 | 800 |
| 5.000 | 1.200.000 | 240 | 1.500.000 | 300 | 540 |
| 6.000 | 1.200.000 | 200 | 1.620.200 | 270 | 470 |
| 8.000 | 1.200.000 | 150 | 2.800.000 | 350 | 500 |
| 10.000 | 1.200.000 | 120 | 4.600.000 | 460 | 580 |
Chceme-li znát náklady na jednotlivý výrobek, můžeme je najít tak, že vypočítáme průměrné fixní náklady a průměrné variabilní náklady a sečteme je dohromady.
Tabulka zahrnuje náklady při šesti odlišných úrovních výroby. Velikost produkce se nalézá v 1. sloupci - vyrobené vozíky, 2. sloupec uvádí celkové fixní náklady. Ty zůstávají při každé výrobní úrovni stejné. Celkové variabilní náklady uvedené ve 4. sloupci se zvyšují s výstupem. 3. a 5. sloupec uvádí průměrné fixní a variabilní náklady. Ty jsou vypočítány vydělením celkových nákladů ve 2. a 4. sloupci počtem vyrobených vozíků (1. sloupec). Průměrné celkové náklady (6. sloupec) uvádějí náklady na výrobu jednotlivého vozíku při každé ze šesti výrobních úrovní. Jsou vypočítány sečtením 3. a 5. sloupce.
Všimli jste si, že zvyšováním počtu vyrobených vozíků se výroba zlevňuje? Jak se výstup dále zvyšuje, klesají náklady na každý vozík. Příčinou je působení dalšího z ekonomických zákonů - zákona klesajících výnosů.
Společnost VAN kupuje kola pro své vozíky od firmy WK. V nedávné studii se ve firmě WK snažili určit, kolik pracovníků firma potřebuje pro provoz své montážní linky na výrobu kol.
Vliv počtu pracovníků na výrobu kol
| Počet | Celkový výstup | Výstup na pracovníka | Příspěvek k celk. výstupu |
|---|---|---|---|
| 1 | 40 | 40 | 40 |
| 2 | 90 | 45 | 50 |
| 3 | 160 | 53,3 | 70 |
| 4 | 260 | 65 | 100 |
| 5 | 320 | 64 | 60 |
| 6 | 360 | 60 | 40 |
| 7 | 380 | 54,3 | 20 |
| 8 | 370 | 46,3 | -10 |
Tabulka říká, že jeden pracovník by sám mohl vyrobit 40 kol za den. Zvýšením na dva pracovníky by se celkový výstup zvýšil na 90 kol, tj. průměr 45 kol na pracovníka.
Zjistilo se také, že přidání jednoho pracovníka zvýší celkový výstup o 50 kol. Ekonomové nazývají dodatečnou jednotku něčeho mezní jednotkou. Tak by mohli říci, že mezní výstup druhého pracovníka na montážní lince ve firmě WK je 50 kol.
Je třeba poznamenat, že zvýšení výstupu nemá co dělat s dovedností dodatečného pracovníka ve srovnání se stávajícím. Spíš ho přivodila lepší „kombinace“ práce a kapitálu.
Se třemi pracovníky se celkový výstup zvýší na 160 kol za den a se čtyřmi činí 260 kol.
Ačkoliv přidáním pátého pracovníka k montážní lince se celkový výstup dále zvyšuje, všimněte si, že tato osoba přidala k celkovému výstupu méně než předcházející. (Zatímco čtvrtý pracovník přidal k celkovému výstupu 100 kol, pátý přidal jen 60.) Podobně se průměrný výstup na pracovníka, který se až do přidání čtvrtého pracovníka zvyšoval, začal snižovat. Ekonomové by to vysvětlili tím, že když byl přidán pátý pracovník k montážní lince, začaly působit klesající výnosy.
Zákon klesajících výnosůProtože celkové fixní náklady zůstávají stejné při každé úrovni výroby, musí se průměrné fixní náklady snižovat se zvyšováním výstupu. Proč se potom průměrné náklady na vozík zvyšují, když firma vyrábí více než 6 000 vozíků ročně?
Odpověď se dotýká vývoje průměrných variabilních nákladů, které (jak vidíte v 5. sloupci tabulky – tabulka v kapitole nahoře) zpočátku klesají a potom se začínají zvyšovat. Pan Vaněk by musel najmout další dělníky a udržovat stroje a jiná zařízení v provozu po delší a delší dobu, aby zvýšil výstup. Nakonec by mohlo být dosaženo bodu, kdy by se dělníci začali plést jeden druhému do cesty, a stroje by začaly vypovídat službu. Stane-li se to, je dosaženo bodu klesajících výnosů a náklady na výrobu každého dalšího vozíku jsou větší než na výrobu toho předchozího.
Ekonomové formulují zákon klesajících výnosů takto: „Jakmile jsou variabilní vstupy (položky, které se započítávají k variabilním nákladům) kombinovány s fixními vstupy (např. budovami a stroji), výstup na jednotku vstupu se zvýší. Avšak pokud proces dále pokračuje, bude dosaženo bodu (bod klesajících výnosů), kdy výstup na jednotku vstupu začne klesat.“
Až dosud jsme se zabývali tím, kolik pana Vaňka stojí výroba jeho vozíků. Zaznamenali jsme, že průměrné náklady na vozíky závisí na tom, kolik jich bylo vyrobeno. Jakmile pan Vaněk měl tuto informaci, mohl zodpovědět velmi důležitou otázku: Kolik vozíků by se mělo vyrábět?
Připomeňme si, že továrna má kapacitu 10 000 vozíků. Produkuje-li továrna 6 000 vozíků ročně, jsou průměrné výrobní náklady na nejnižší úrovni (470 Kč za vozík). – tabulka v kapitole výše Měl by pan Vaněk vyrábět 6 000 vozíků nebo více? Počet vozíků, které bude pan Vaněk pravděpodobně vyrábět, bude záviset na tom, kolik jich může prodat. Pan Vaněk jako každý moudrý výrobce ví, že množství vozíků, které by měl vyrobit, bude určováno zákonem nabídky a poptávky.
Počet vozíků, které může prodat, bude částečně záviset na jejich prodejní ceně. Z nedávného přehledu trhu se zaměstnanci VAN dozvěděli o vlivu prodejní ceny na poptávku po jejich výrobku.
Tabulka poptávky po vozících
| Při ceně | Počet vozíků, které by byly prodány |
|---|---|
| 1 000 | 1 000 |
| 900 | 3 000 |
| 800 | 5 000 |
| 700 | 6 000 |
| 600 | 8 000 |
| 500 | 10 000 |
Když účetní aplikoval tyto informace na svou dřívější studii nákladů, byl schopen vyvodit závěry o vlivu prodejní ceny na zisk nebo ztrátu.
| Při ceně | Vyrob. a prod. vozíky | Celk. fixní náklady | Prům. fixní náklady | Celk. variab. náklady | Prům. variab. náklady | Průměrné celkové náklady | Jedn. zisk (ztráta) | Celkový zisk (ztráta) |
|---|---|---|---|---|---|---|---|---|
| 1000 | 1000 | 1.200.000 | 1200 | 700.000 | 700 | 1900 | (900) | (900.000) |
| 900 | 3000 | 1.200.000 | 400 | 1.200.000 | 400 | 800 | 100 | 300.000 |
| 800 | 5000 | 1.200.000 | 240 | 1.500.000 | 300 | 540 | 260 | 1.300.000 |
| 700 | 6000 | 1.200.000 | 200 | 1.620.000 | 270 | 470 | 230 | 1.380.000 |
| 600 | 8000 | 1.200.000 | 150 | 2.800.000 | 350 | 500 | 100 | 800.000 |
| 500 | 10000 | 1.200.000 | 120 | 4.600.000 | 430 | 580 | (80) | (800.000) |
Jak je uvedeno v tabulce, prodejní cena 700 Kč za vozík a úroveň výroby ve výši 6 000 vozíků budou přinášet firmě největší zisk 1 380 000 Kč.
Úspory z rozsahuMetody zaměřené na zvýšení výkonnosti, jako je dělba práce, úzká specializace pracovníků na určité činnosti, používání nákladných výrobních zařízení a montážních linek apod. jsou nejefektivnější ve velkých provozech. Jak velká musí firma být, aby se jí vyplatilo používat tyto metody, to se liší případ od případu. Jakmile však firma této velikostí dosáhne, říkají ekonomové, že začíná využívat úspor z rozsahu (snížení nákladů vyplývajících z výroby ve velkém měřítku).
Firmy dosahují úspor z rozsahu tím, že využívají následujících možností:mohou nakupovat v množstvích, která je opravňují ke slevám při nákupu surovin
mohou si dovolit koupit specializované stroje a zařízení, aby snížily jednotkové náklady
mohou si dovolit investovat do programů výzkumu a vývoje, které společnostem umožňují snížit výrobní náklady a produkovat nové a zlepšené výrobky
mohou si dovolit využít všech výhod dělby práce
